About two years ago I wrote about a category-theoretic treatment of collaborative text editing. That post is unique in the history of Bosker Blog in having been cited – twice so far that I know of – in the academic literature; so it’s a little embarrassing for me to have to explain that it is almost entirely wrong. The good news is that the core idea can be rescued, and the corrected story is quite interesting. Other writers on this subject seem to have made at least some of the same mistakes I did, so I hope this will be useful to at least a few other people too.
I was considering the problem of collaborative text editing, where several people separately and simultaneously are editing the same document and communicating their changes asynchronously to each other:
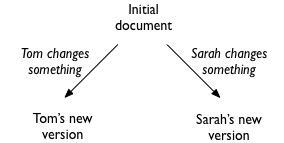
Each editor must then incorporate the other’s change into their version of the document, which must be done in such a way that they both end up with the same thing:
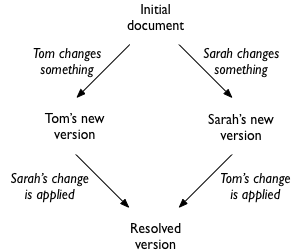
The hard case is where Tom and Sarah’s changes overlap: say they have both changed the same word to something different. In the example I used, the document read “The cat sat on the mat”, and they both select the word cat:
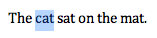
Then Tom types ‘dog’, and Sarah types ‘chicken’. This appears to be unresolvable if we require our documents to be linear – but we can achieve a canonical resolution if we permit non-linear documents:

In general the resolved document contains all the characters that neither editor changed, together with all the characters inserted by Tom and all the characters inserted by Sarah, ordered in the minimal way that is consistent with both documents.
So far so good. Now it starts to go wrong. There are two fundamental problems: pushouts imply pathological documents, and deletions lead to disaster. In turn:
Pushouts imply pathological documents
I said this resolution was a pushout in a category of edits. That is not true as I stated it, and moreover I think the examples show that we don’t want it to be true.
My previous example will not do here, since “dog” and “chicken” have no letters in common. Let us suppose, then, that instead of dog and chicken we have badger and donkey:

Let us recall what it means for the resolution to be a pushout. Start with a document that we shall call A, and suppose that, simultaneously:
- Tom makes an edit, call it f, resulting in the document B;
- Sarah makes an edit, call it g, resulting in the document C.
These edits are propagated: both parties run the resolution algorithm, and then Tom applies Sarah’s edit and Sarah applies Tom’s. Let’s label the resolved version of f as f’, the resolved version of g as g’, and the resulting document P.
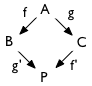
[…]
Now, the properties of the pushout require that, given any resolution of the two edits (“The donkey sat…” and “The badger sat…”) there must be a unique edit from the pushout to this other resolution. One possible resolution would be to insert letters into the name of the animal to make “badonkeyger”:

In other words, the properties of the pushout require us to admit an edit that takes the parallel donkey/badger and flattens it out, identifying the two d’s.
This seems perverse. It certainly is not in line with my intuition about what sorts of edits ought to be permissible. But it gets worse! By admitting these strange edits that merge letters from parallel tracks, we have opened the door to yet stranger things such as cyclic documents. Consider the following pair of edits that merge two parallel tracks. The bold pink d in badonkeydonkger indicates the image of the ‘d’ in badger: it could have been merged with either of the two d’s in donkeydonk. Resolving this pair of edits will necessarily create a cyclic document.
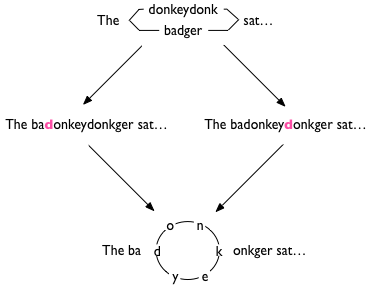
Samuel Mimram and Cinzia Di Giusto’s article A Categorical Theory of Patches – rather like my earlier On Editing Text – develops a theory where edits are resolved as pushouts. Unlike me, however, they recognised this issue, which they deal with by admitting cyclic documents into their theory. I shall take the alternative approach of arguing that, on the contrary, these examples show that pushouts do not correctly model edit resolution.
It’s okay that our resolutions are not pushouts, because they still have the property we really wanted in the first place: that edits can be resolved in any order and give the same answer. (And it’s good that they’re not, because if they were we would have to admit circularities etc.)
Deletions lead to disaster
The second problem is worse, because we get different answers depending on what order we process the edits. To resolve it we’ll have to change the way we represent deletions.
We’ll start with the document “ABC” and consider three different edits of this document:
- Insert v and w to get “AvBwC”;
- Insert x and y to get “AxByC”;
- Delete the B to get “AC”.
Now, combining (1) and (2) gives:
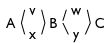
And combining that with (3) gives:

On the other hand, if we resolved these edits in a different order then we get a different answer. Combining (1) and (3) gives “AvwC”, then combining that with (2) gives:
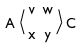
So this resolution procedure is not order-independent, which is very bad. In particular it cannot be a pushout, which I believe shows that Mimram and Di Giusto’s Theorem 20 is false.
Avoiding deletions using tombstones
We can avoid this problem by not allowing characters to be deleted. When a user deletes a character, rather than removing it from the internal representation of the document, replace it with a tombstone marking where the character used to be.
We don’t need to keep these tombstones around for ever, I don’t think. Once we’re sure that an edit has been incorporated by all clients, there is no harm in discarding the tombstones it produced.
An object of the category – a document – is a triple (A, ≤, s) where (A, ≤) is the poset of positions and s: A → Σ assigns a symbol to each position.
A morphism f: A→B is a function such that for all x, y in A:
- x ≤ y ⇔ f(x) ≤ f(y)
- Either s(f(x)) = s(x) or s(f(x)) is a tombstone.
The resolution R of f: A→B and g: A→C has positions A + (B-f[A]) + (C-g[A]). Note that A + (B-f[A]) is isomorphic to B, and A + (C-g[A]) is isomorphic to C. The order of positions is inherited from B and C:
- If b ≤ b’ in B then b ≤ b’ in R
- If c ≤ c’ in C then c ≤ c’ in R
- b ≤ c, for b∈B and c∈C, if there is some a∈A such that b ≤ f(a) in B and g(a) ≤ c in C
- c ≤ b, for b∈B and c∈C, if there is some a∈A such that c ≤ g(a) in C and f(a) ≤ b in B
The assignment of characters to positions is:
- sR(b) = sB(b) for b∈B,
- sR(c) = sC(c) for c∈C,
- sR(a) is a tombstone if either sB(f(a)) or sC(g(a)) is; otherwise sR(a) = sB(f(a)) = sC(g(a)).
What about the connection to the exception monad?
As I understand the situation at the moment, that doesn’t work. Constructing the category of edits in that way seems to rely on having real deletions – which we’ve seen we can’t have.

Pingback: On editing text | Bosker Blog
I don’t think pushouts are bad in the way that you say. Let’s we start with a document “The sat”. I edit it to “The x sat” and you also edit it to “The x sat”. The pushout of our patches is not just “The x sat”, rather it is “The sat” where denotes that the ordering relation does not order the two x’s. This is because you could patch yours to “The xerxes sat”, adding “erxes” between “x” and ” sat”, and I could patch mine to “The xerxes sat”, adding “xer” and “es” on either side of “x”. These two patches do not factor through the patches that send both our patches to the same string “The x sat”, because this single “x” in “The x sat” couldn’t be sent to both “x”s in “xerxes” at the same time by a single map. The same logic applies to your example about “donkey” and “badger”. The “d”s must be duplicated in the pushout, or the pushout is not sufficiently universal.
Another thing: we can’t know a patch just by knowing the source string and the target string. The string “a” could be changed into “aa” in three different ways: adding an “a” at the end, adding an “a” at the beginning, or deleting an “a” and adding “aa”. This is why the Mimram and Di Guisto paper models patches as partial injective monotonic functions that preserve letter assignments. I think git determines a patch just from the source and target string, which means that some patches are impossible for it to represent. (I’m not sure about it’s algorithm). I just wanted to point this out because in your post you usually talk about a patch just in terms of the source and target strings, and this might have been the source of the above confusion.
I’m so sorry it’s taken me almost seven years to reply to this!
I agree with everything you say here, but I think you must have misunderstood what I meant by my example. I intended only to argue that there must exist a map that identifies the letters on parallel tracks. (Not that the pushout itself would identify them, which as you say it does not.)
I can’t help but see a similarity to problems of geometry, where we’re trying to lift the solution of a local problem (= choose a resolution for a character) to a global one (= choose a resolution for a document).
The model for such situations is given by sheaves. On a topological space X, a sheaf is an assignment F between open sets U of X and object F(U) in a chosen category (usually of modules, more generally any “abelian category”). Moreover, they need to satisfy additional requirements suggested by the situation: they must be compatible with restrictions and with glueing operations (in categorical lingo, they are contravariant functors with “nice” extra properties, as they transfer the lattice structure of open sets to the target category).
Usually, geometry deals with sheaves given by modules of functions from some object X to a ring, like smooth functions from any open set U of a manifold to the reals, or vector fields, or differential forms, etc. All these objects I cited are said to be ‘sections’ of their sheaf. If they’re defined on an open set, they’re ‘local sections’, and if this open set is the whole space then they’re ‘global sections’. A lot of geometry can be condensed down to the problem of finding a way to extend local sections to global sections, for a certain sheaf.
I believe we can adopt a sheaf-theoretic perspective of the edits, too.
We can imagine a document to a sheaf D of functions from a subset U of the natural numbers (considered as a discrete topological space) to strings of chars and tombstone. We simply say D(U) is given by the function assigning chars to the elements of U, e. g. if U = {1,2,3}, D(U) could be “T h e”.
Indeed, it’s easy to see the natural compatibility conditions are satisfied: any restriction of subsets gives a morphism D(U) -> D(V) by restrict the function itself. Glueing works as well: if we have a function “a b c” in D({1,2,3}) and another one “c d e” in D({3,4,5}) then there’s also a function “a b c d e” in D({1,2,3,4,5}). All the other ones I didn’t state before are trivially satisfied as well.
Then can we model an edit as a morphism of sheaves? The general definition of such a morphism is just a specialization of that of natural transformation, since we’ve said sheaves are particular functors. Specialized in this case, a morphism let F and G be sheaves on X. A morphism from F to G is given by a map F(U) -> G(U) (in the target category (in our case, that of partial functions from the naturals to a set of chars) for each open U of X, such that a compatibility condition is satisfied: let U and V be open sets in X, such that V is contained in U, then we want this to commute:
F(U) – – > F(V)
| |
v v
G(U) – – > G(V)
Can such a notion model that of a document edit? Probably so. Indeed, unpacking the definition we just gave, we see that a morphism of documents would be a reassignment of the chars F assigns to U to the chars of G.
I swept under the carpet the exact definition of the target category of the documents, but by now you should be able to figure it out. It is the category of maps U -> A where U is a subset of the naturals and A is the alphabet we are using, whose morphisms are maps U – > V and A -> A making the obvious square commute (such a category is somewhat related to the more familiar “category of objects over A”, but there’s a fundamental difference I’ll let you find).
Now for the magic trick.
Notice that edits of a fixed document A form themselves a sheaf over N, by obvious generalizations of our definitions (in particular, we define ‘local documents’ to be documents on a subset U and ‘local edits’ are just morphisms of the former).
Then the problem of finding a resolution of a document can be stated as a local-global problem: given two edits A->B and A->C, can we get a document D agreeing with both B and C?
The answer is obviously _no_ since this is possible only when B=C. However, locally we see this is a much easier problem: we just need to find a subset on which B agrees with C, and then this local document is a local solution. Hence our resolution problem becomes a local-to-global problem: can we extend our local solution to a global one?
Again, the answer is still _no_, but so is in geometry. To understand why extension fails however, geometers went to great lengths and invented all sorts of sheaf-theoretic machineries. The most important is called sheaf cohomology and given two sheaves B and C produces a number of groups telling us how sections of C which locally come from sections of B fails to do that globally. Set B=C and you get a local-to-global extension problem.
I rambled way to much for now. I do not know if the thing above is consistent or I swept under the carpet too many things. I can already see there as to be a better definition of edit since now equivalent edits are not things you would consider equivalent IRL, so there has to be a better notion. Moreover, my proposed gadget to handle resolution is defined for abelian sheaves, so basically we need our category of edits to be abelian, which is a strong property I’m quite sure it doesn’t have.
Eventually, the take away I wanted to give was that sheaves could be a better model for documents and edits, due to their intrinsic ability to model local-to-global problems.