Superpermutations: lower bound

I wrote about superpermutations here: a superpermutation is a string that has as substrings all the permutations of some set of symbols.

For example, there are six permutations of the symbols 1, 2, 3. They are: 123, 132, 213, 231, 312, 321. The string 123121321 has all six of these as substrings – and it’s the shortest string that does, with only one three-character substring that isn’t a permutation: the 121 in the middle.

For larger numbers of symbols it’s impossible to do quite so well. For example, there are 24 different permutations of the symbols 1, 2, 3, 4, and the shortest superpermutation is 123412314231243121342132413214321, which has 33 characters. So there are 30 different four-character substrings, and six of them contain repeated symbols: 1231, 2312; 3121 and 1213 (which overlap with each other); 2132, and 1321.

Here it is again, with the non-permutations highlighted:

123412314231243121342132413214321

No general formula is known for the length of the shortest superpermutation on n symbols. If we denote this length s(n), then it is known that for n ≥ 3,

and it is known that neither bound is tight in general. We know the lower bound is not tight because s(5) has been computed exactly and is equal to 153, whereas the formula for the lower bound gives 152. We know the upper bound is not tight because there are superpermutations on 6 symbols of length 872, so we know that s(6) ≤ 872, whereas the formula for the upper bound gives 873.

Squares of squares, and the group of rational points on the circle

The purpose of this post is to describe a slightly different way of thinking about the existence – or otherwise – of a 3×3 magic square of squares. Of course it may not lead to any real progress, but it does at least suggest some natural weaker questions that may be more amenable. It follows on from part 1 and part 2.

Almost-magic squares of squares

In the last post we saw that every 3×3 almost-magic square is a rearrangement of three three-term arithmetic progressions that have the same common difference. In other words, if we pick any three numbers x, y and z, and any common difference d, then the nine numbers

x–d,	x,	x+d
y–d,	y,	y+d
z–d,	z,	z+d

can be rearranged to make an almost-magic square

x	z+d	y-d
z-d	y	x+d
y+d	x-d	z

where all the rows and columns, and the leading diagonal, add up to x+y+z.

We’re interested in finding almost-magic squares where all the entries are square numbers, so that means we’re particularly interested in three-term arithmetic progressions of squares. Fortunately there is a well-developed theory of these things, which are closely related to Pythagorean triples.

Magic squares of squares: Part I

A recent Numberphile video discussed an intriguing unsolved problem in number theory: is there a 3×3 magic square whose entries are all square numbers? (Matt Parker proposed a solution which doesn’t quite work: see the video for more. The “Parker square” even has its own Twitter account.)

It turns out that this question leads to some interesting mathematics, which I’m going to have a go at explaining. At the very least I hope to give some insight into why it’s a hard problem.

To reduce the risk that I’ll run out of time and energy before pressing Publish, I’m going to split this post into two or possibly three parts, which I’ll post separately. The first part, which you’re reading right now, gives some background on 3×3 magic squares. The second will explain how to find almost-magic squares of squares using a bit of number theory and computer algebra. By almost-magic I mean that the rows and the columns and one of the two diagonals have the same sum.

The third, if I write it, will be more speculative and look at some possible approaches to either finding the mythical square of squares or proving that it doesn’t exist.

Counting coins

This afternoon, Matt Locke tweeted the following problem from his nine-year-old daughter’s maths homework:

The Government Statistical Service’s terrible spreadsheet advice

The UK Government Statistical Service recently released its good practice guidance for releasing statistics in spreadsheets. While this advice is clearly well-intentioned^*, and parts of it are good, the overall effect is to encourage the release of data in formats that are difficult to process by computer. This is a disappointing retrograde step.

Tackling the Minimal Superpermutation Problem

What’s the shortest string that contains every possible permutation of ABCD somewhere inside it? As it happens, it’s 33 letters long: ABCDABCADBCABDCABACDBACBDACBADCBA. A string like this is called a minimal superpermutation.

So what’s the shortest string that contains every possible permutation of ABCDE? It was recently shown that 153 letters is the shortest possible, and that there are eight different superpermutations of this length.

Okay, what about ABCDEF? The answer is that nobody knows. Until this week the shortest known superpermutation of ABCDEF was 873 letters long:

ABCDEFABCDEAFBCDEABFCDEABCFDEABCDFEABCDAEFBCDAEBFCDAEBCFDAEBCDFAEB
CDAFEBCDABEFCDABECFDABECDFABECDAFBECDABFECDABCEFDABCEDFABCEDAFBCED
ABFCEDABCFEDABCADEFBCADEBFCADEBCFADEBCAFDEBCADFEBCADBEFCADBECFADBE
CAFDBECADFBECADBFECADBCEFADBCEAFDBCEADFBCEADBFCEADBCFEADBCAEFDBCAE
DFBCAEDBFCAEDBCFAEDBCAFEDBCABDEFCABDECFABDECAFBDECABFDECABDFECABDC
EFABDCEAFBDCEABFDCEABDFCEABDCFEABDCAEFBDCAEBFDCAEBDFCAEBDCFAEBDCAF
EBDCABEFDCABEDFCABEDCFABEDCAFBEDCABFEDCABACDEFBACDEBFACDEBAFCDEBAC
FDEBACDFEBACDBEFACDBEAFCDBEACFDBEACDFBEACDBFEACDBAEFCDBAECFDBAECDF
BAECDBFAECDBAFECDBACEFDBACEDFBACEDBFACEDBAFCEDBACFEDBACBDEFACBDEAF
CBDEACFBDEACBFDEACBDFEACBDAEFCBDAECFBDAECBFDAECBDFAECBDAFECBDACEFB
DACEBFDACEBDFACEBDAFCEBDACFEBDACBEFDACBEDFACBEDAFCBEDACFBEDACBFEDA
CBADEFCBADECFBADECBFADECBAFDECBADFECBADCEFBADCEBFADCEBAFDCEBADFCEB
ADCFEBADCBEFADCBEAFDCBEADFCBEADCFBEADCBFEADCBAEFDCBAEDFCBAEDCFBAED
CBFAEDCBAFEDCBA

and it was thought that might be the shortest possible.

But we now know it isn’t, because I found a shorter one:

ABCDEFABCDEAFBCDEABFCDEABCFDEACBFDEACFBDEACFDBEACFDEBACFDEABCDFEAB
CDAEFBCDAEBFCDAEBCFDAEBCDFAEBCDAFEBCDABEFCDABECFDABECDFABECDAFBECD
ABFECDABCEFDABCEDFABCEDAFBCEDABFCEDABCFEDACBFEDCABFDECAFBDCEAFBDCA
EFBDCAFEBDCAFBEDCAFBDECAFDBECADFBECADBFECADBEFCADBECFADBECAFDEBCAD
FEBCADEFBCADEBFCADEBCFADEBCAFDECBAFDECABFDCEABFDCAEBFDCABEFDCBAEFD
BCAEDFBCAEDBFCAEDBCFAEDBCAFEDBCAEFDBACEFDBAECFBDAECFBADECFBAEDCFBA
ECDFBACEDFBACDEFBACDFEBACDFBEACDFBAECFDBAEFCDBAFECDBAFCEDBAFCDEBAF
CDBEAFCDBAEFDCBEAFDCBEFADCBEFDACBEFDCABFEDCBAFEDCBFAECDBFACEDBFACD
EBFACDBEFACDBFEACDBFAECBDFEACBDFECABDFCEABDFCAEBDFCABEDFCBAEDFCBEA
DFCBEDAFCBEDFACBEDFCABDEFCBADEFCBDAEFCBDEAFCBDEFACBDEFCABDFECBADFE
CBDAFECBDFAECBFDAECBFADECBFAEDCBFEADCFBEADCFEBADCEFBADCEBFADCEBAFD
CEBADFCEBADCFEABDCFAEBDCFABEDCFABDECFABDCEFABDCFEADBCEFADBCEAFDBCE
ADFBCEADBFCEADBCFEADCBFEDACFBEDACFEBDACEFBDACEBFDACEBDFACEBDAFCEBD
ACFEDBACFEDABC

I’ve uploaded a short note about it to the arxiv.

Revisiting “On editing text”

About two years ago I wrote about a category-theoretic treatment of collaborative text editing. That post is unique in the history of Bosker Blog in having been cited – twice so far that I know of – in the academic literature; so it’s a little embarrassing for me to have to explain that it is almost entirely wrong. The good news is that the core idea can be rescued, and the corrected story is quite interesting. Other writers on this subject seem to have made at least some of the same mistakes I did, so I hope this will be useful to at least a few other people too.

I was considering the problem of collaborative text editing, where several people separately and simultaneously are editing the same document and communicating their changes asynchronously to each other:

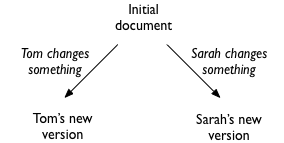
Each editor must then incorporate the other’s change into their version of the document, which must be done in such a way that they both end up with the same thing:

The hard case is where Tom and Sarah’s changes overlap: say they have both changed the same word to something different. In the example I used, the document read “The cat sat on the mat”, and they both select the word cat:

Then Tom types ‘dog’, and Sarah types ‘chicken’. This appears to be unresolvable if we require our documents to be linear – but we can achieve a canonical resolution if we permit non-linear documents:

In general the resolved document contains all the characters that neither editor changed, together with all the characters inserted by Tom and all the characters inserted by Sarah, ordered in the minimal way that is consistent with both documents.

So far so good. Now it starts to go wrong. There are two fundamental problems: pushouts imply pathological documents, and deletions lead to disaster. In turn:

Pushouts imply pathological documents

I said this resolution was a pushout in a category of edits. That is not true as I stated it, and moreover I think the examples show that we don’t want it to be true.

My previous example will not do here, since “dog” and “chicken” have no letters in common. Let us suppose, then, that instead of dog and chicken we have badger and donkey:

Let us recall what it means for the resolution to be a pushout. Start with a document that we shall call A, and suppose that, simultaneously:

• Tom makes an edit, call it f, resulting in the document B;
• Sarah makes an edit, call it g, resulting in the document C.

These edits are propagated: both parties run the resolution algorithm, and then Tom applies Sarah’s edit and Sarah applies Tom’s. Let’s label the resolved version of f as f’, the resolved version of g as g’, and the resulting document P.

[…]

Now, the properties of the pushout require that, given any resolution of the two edits (“The donkey sat…” and “The badger sat…”) there must be a unique edit from the pushout to this other resolution. One possible resolution would be to insert letters into the name of the animal to make “badonkeyger”:

 

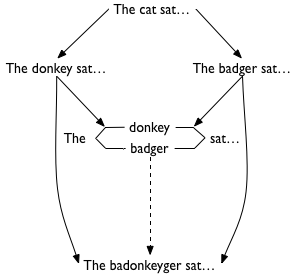
In other words, the properties of the pushout require us to admit an edit that takes the parallel donkey/badger and flattens it out, identifying the two d’s.

This seems perverse. It certainly is not in line with my intuition about what sorts of edits ought to be permissible. But it gets worse! By admitting these strange edits that merge letters from parallel tracks, we have opened the door to yet stranger things such as cyclic documents. Consider the following pair of edits that merge two parallel tracks. The bold pink d in badonkeydonkger indicates the image of the  ‘d’ in badger: it could have been merged with either of the two d’s in donkeydonk. Resolving this pair of edits will necessarily create a cyclic document.

Samuel Mimram and Cinzia Di Giusto’s article A Categorical Theory of Patches – rather like my earlier On Editing Text – develops a theory where edits are resolved as pushouts. Unlike me, however, they recognised this issue, which they deal with by admitting cyclic documents into their theory. I shall take the alternative approach of arguing that, on the contrary, these examples show that pushouts do not correctly model edit resolution.

It’s okay that our resolutions are not pushouts, because they still have the property we really wanted in the first place: that edits can be resolved in any order and give the same answer. (And it’s good that they’re not, because if they were we would have to admit circularities etc.)

Deletions lead to disaster

The second problem is worse, because we get different answers depending on what order we process the edits. To resolve it we’ll have to change the way we represent deletions.

We’ll start with the document “ABC” and consider three different edits of this document:

1. Insert v and w to get “AvBwC”;
2. Insert x and y to get “AxByC”;
3. Delete the B to get “AC”.

Now, combining (1) and (2) gives:

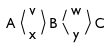
And combining that with (3) gives:

On the other hand, if we resolved these edits in a different order then we get a different answer. Combining (1) and (3) gives “AvwC”, then combining that with (2) gives:

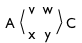
So this resolution procedure is not order-independent, which is very bad. In particular it cannot be a pushout, which I believe shows that Mimram and Di Giusto’s Theorem 20 is false.

Avoiding deletions using tombstones

We can avoid this problem by not allowing characters to be deleted. When a user deletes a character, rather than removing it from the internal representation of the document, replace it with a tombstone marking where the character used to be.

We don’t need to keep these tombstones around for ever, I don’t think. Once we’re sure that an edit has been incorporated by all clients, there is no harm in discarding the tombstones it produced.

An object of the category – a document – is a triple (A, ≤, s) where (A, ≤) is the poset of positions and s: A → Σ assigns a symbol to each position.

A morphism f: A→B is a function such that for all x, y in A:

1. x ≤ y ⇔ f(x) ≤ f(y)
2. Either s(f(x)) = s(x) or s(f(x)) is a tombstone.

The resolution R of  f: A→B and  g: A→C has positions A + (B-f[A]) + (C-g[A]). Note that A + (B-f[A]) is isomorphic to B, and A + (C-g[A]) is isomorphic to C. The order of positions is inherited from B and C:

• If b ≤ b’ in B then b ≤ b’ in R
• If c ≤ c’ in C then c ≤ c’ in R
• b ≤ c, for b∈B and c∈C, if there is some a∈A such that b ≤ f(a) in B and g(a) ≤ c in C
• c ≤ b, for b∈B and c∈C, if there is some a∈A such that c ≤ g(a) in C and f(a) ≤ b in B

The assignment of characters to positions is:

• s_R(b) = s_B(b) for b∈B,
• s_R(c) = s_C(c) for c∈C,
• s_R(a) is a tombstone if either s_B(f(a)) or s_C(g(a)) is; otherwise s_R(a) = s_B(f(a)) = s_C(g(a)).

What about the connection to the exception monad?

As I understand the situation at the moment, that doesn’t work. Constructing the category of edits in that way seems to rely on having real deletions – which we’ve seen we can’t have.

Decoding the mysterious symmetry of the bicycle lock numbers

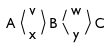
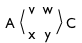
Suppose you have a lock of this sort that has n dials and k numbers on each dial. Let m(n, k) be the minimum number of turns that always suffice to open the lock from any starting position, where a turn consists of rotating any number of adjacent rings by one place.

In the previous post, we found an algorithm for computing these bicycle lock numbers, revealing a mysterious symmetry,

The bicycle lock problem

Photo: WickedVT

Don’t lock your bicycle with a combination lock. Someone will steal it: I learnt this the hard way. It’s quite easy to open a combination lock by feel, without knowing the combination. Try it: with a bit of practice, you can open the lock with your eyes shut. (It’s easier to do this with an old wobbly lock than a tight-fitting new one.)