Games I

When I started doing research, I mostly worked on categories of games. I even went so far as to write a first-year report that suggested — even confidently claimed — that I would write a thesis on the subject. Well, I’m writing that thesis now, and games appear only in passing in a single paragraph. But recently, one or two people have expressed some interest in some of the ideas in that first-year report, so I’d like to flesh out one of idea that is only sketched very vaguely in what I wrote.

The starting point is the idea that a simple category of games is (equivalent to) the initial model of a certain simple theory. Before I explain, I should make it clear that this observation is not original: it’s really just a different way of thinking about some of the ideas of Polarized category theory, modules, and game semantics (Cockett and Seely).

Say that a lift operator on a category $\mathbb{C}$ is a functor $\mathop\uparrow: \mathbb{C} \to\mathbb{C}^\mathrm{op}$ , self-adjoint on the right. That means there is a natural isomorphism

$\mathbb{C}(X, \mathop\uparrow Y)\cong\mathbb{C}(Y, \mathop\uparrow X)$

or alternatively that there is a natural isomorphism $\eta$ — the unit of the adjunction — with components

$\eta_X: X\to\mathop\uparrow\mathop\uparrow X$

such that the composite

$\mathop\uparrow X \mathrel{\mathop{\longrightarrow}\limits^{\eta_{\mathop\uparrow X}}}\mathop\uparrow\mathop\uparrow\mathop\uparrow X \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow\eta_X}} \mathop\uparrow X$

is the identity.

Now say that an lp-category is a category equipped with a lift operator and finite products. I claim that the initial lp-category is equivalent to the category of finite, simple games, with deterministic, winning strategies.

There’s a little subtlety here, which perhaps is worth mentioning. Products are defined in a non-algebraic way, by a universal property, but if we want to talk about the initial model then we need our structure to be algebraic. This issue is usually glossed over, because there is an easy way of dealing with it — at least if you believe in the axiom of choice. If you choose a product cone for each pair of objects, and you choose a terminal object, these choices suffice to determine a unique monoidal structure representing the product; a functor strictly preserves this monoidal structure just when it takes each chosen product cone to a chosen product cone in the target. It’s actually more convenient for us to have easy access to $n$ -ary products for arbitrary finite $n$ , so we shall go further and insist that a product cone be chosen for every finite set of objects. (This gives rise to what Tom Leinster calls an unbiased monoidal structure on the category.)

Having found a suitably algebraic notion of lp-category, there is clearly an initial such thing, by the usual syntactic shenanigans. Let’s call it $\mathbf{LP}$ . Every object of $\mathbf{LP}$ is isomorphic to one of the form

$\prod_{i\in I} \mathop\uparrow A_i$

where each $A_i$ is of the same form, recursively. (The recursion is grounded by the empty product, i.e. the terminal object, which we’ll write as $1$ .)

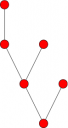
Thus the objects of $\mathbf{LP}$ correspond to finite trees. For example, the object $\mathop\uparrow(\mathop\uparrow\mathop\uparrow1\times\mathop\uparrow1) \times \mathop\uparrow1$ can be drawn as

Now, the claim is that a morphism $X\to Y$ in $\mathbf{LP}$ is a total strategy for the game $X\multimap Y$ , where the trees $X$ and $Y$ are regarded as games.

It’s pretty clear that at least some of the morphisms of $\mathbf{LP}$ correspond to strategies in a reasonably simple way. I’ll give a recursive definition of “strategic” morphisms:

Given a collection $(f_i: A \to \mathop\uparrow B_i)$ of strategic morphisms, the tuple $\langle f_i\rangle: A \to \prod_i \mathop\uparrow B_i$ is strategic. (In particular the case where the collection is empty implies that the unique map $A \to 1$ is strategic, which constitutes a base case for the recursion.) This represents the strategy where, when the opening O-move is in component $i$ , we then play according to strategy $f_i$ .
Given a collection of objects $(X_i | i \in I)$ , and a strategic morphism $f: A \to X_n$ for some $n \in I$ , the composite
$\prod_i \mathop\uparrow(X_i)\mathrel{\mathop{\longrightarrow}\limits^{\pi_n}} \mathop\uparrow X_n\mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow f}}\mathop\uparrow A$

is strategic. This is the strategy in which the (unique) opening O-move is replied to in component ‘ $n$ ‘ on the left, and then play continues according to the strategy $f$ .
Given a collection of objects $(Y_i | i \in I)$ , and a strategic morphism $f: A \to Y_n$ for some $n \in I$ , the composite
$A \mathrel{\mathop{\rightarrow}\limits^f}Y_n\mathrel{\mathop{\longrightarrow}\limits^{\eta_{Y_n}}} \mathop\uparrow\mathop\uparrow Y_n\mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow\pi_n}}\mathop\uparrow(\prod_i\mathop\uparrow Y_i)$

is strategic. This corresponds to the strategy in which the opening O-move is replied to in component ‘ $n$ ‘ on the right, and then play continues according to $f$ .

All that remains is to show that every morphism is strategic. It’s easy enough to show that every identity morphism is strategic, by induction over the tree structure of the object and using rules 1 and 2. It’s also immediate that the basic morphisms $\eta_A$ and the projections are strategic and 2 implies in particular that the lift of a strategic morphism is strategic. It is trivial to show, using 1, that the strategic morphisms are closed under tupling. Hence it remains only to show that the composite of two strategic morphisms is strategic.

Now, most of the cases are trivial. The one that isn’t is the case of a tuple of 3-maps followed by a 2-map. (Of course this is the case where play continues on the hidden board, so you’d expect this to be the interesting case.) The projection extracts one of the elements of the tuple, so it amounts to considering the composite

$A \mathrel{\mathop{\longrightarrow}\limits^{f}} Y_n \mathrel{\mathop{\longrightarrow}\limits^{eta_(Y_n)}} \mathop\uparrow \mathop\uparrow Y_n \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow \pi_n}} \mathop\uparrow (\prod_i \mathop\uparrow Y_i) \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow g}} \mathop\uparrow B$

where $f$ and $g$ are strategic. Since $g$ is a map into a product, we can go further and extract the appropriate component of $g$ , which is clearly also strategic, so it suffices to show that the composite

is strategic whenever $f$ and $g$ are. This may be proved by induction over $g$ : if $g$ is of type 2, then we have

$A \mathrel{\mathop{\longrightarrow}\limits^{f}} Y \mathrel{\mathop{\longrightarrow}\limits^{\eta_Y}} \mathop\uparrow \mathop\uparrow Y \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow \mathop\uparrow h}} \mathop\uparrow \mathop\uparrow B_n \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow pi_n}} \mathop\uparrow \prod_i \mathop\uparrow B_i$

which, by naturality of $\eta$ , is of type 3. If $g$ is of type 3, then we have $Y = \prod_i \mathop\uparrow Y_i$ , and the map is

$A \mathrel{\mathop{\longrightarrow}\limits^{f}} Y \mathrel{\mathop{\longrightarrow}\limits^{\eta_Y}} \mathop\uparrow \mathop\uparrow Y \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow \mathop\uparrow \pi_n}} \mathop\uparrow \mathop\uparrow \mathop\uparrow Y_n \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow\eta_(Y_n)}} \mathop\uparrow Y_n \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow h}} \mathop\uparrow B$

for some $h$ that is simpler than $g$ . Using the naturality of $\eta$ and the adjunction triangle, this is

$A \mathrel{\mathop{\longrightarrow}\limits^{f}} Y \mathrel{\mathop{\longrightarrow}\limits^{\pi_n}} \mathop\uparrow Y_n \mathrel{\mathop{\longrightarrow}\limits^{\mathop\uparrow h}} \mathop\uparrow B$

and the inductive hypothesis applies.

This is getting long, so I’ll continue the story in another post.

Games I

1 Response to Games I

Leave a comment Cancel reply

Archives

Meta

Games I

Share this:

Related

1 Response to Games I

Leave a comment Cancel reply

Archives

Meta